PID-Regler
1 Was ist ein PID-Regler?
Ein PID-Regler (aus dem Englischen: Proportional Integral Derivative Controller) ist ein Rückkopplungsmechanismus des Regelkreises, der in industriellen Steuerungssystemen genutzt wird. Ein PID-Regler berechnet ständig einen Fehlerwert, der die Differenz zwischen der gemessenen Prozessgröße und dem gewünschten Sollwert berechnet. Die Steuerung versucht den Fehler durch die Anpassung der Regelgröße, wie die Position des Regelventils, des Dämpfers oder der Stromzufuhr des Heizelements zu minimalisieren.
(Übersetzung aus Auszügen Wikipedia EN: PID controller)
2 Reglerstrukturen (Darstellungsmöglichkeiten)

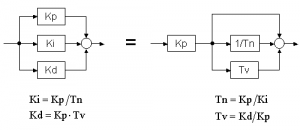
Es gibt zwei Darstellungsmöglichkeiten, die inhaltlich identisch sind. In der analogen Regeltechnik ist noch die Darstellung mit der Nachstellzeit Tn und der Vorhaltezeit Tv üblich. Die Umrechnung zwischen den beiden Strukturen ist mit den angegebenen Formeln möglich.
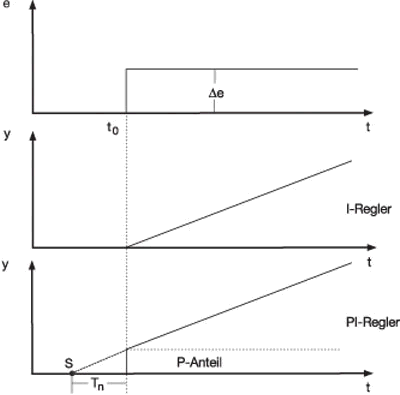
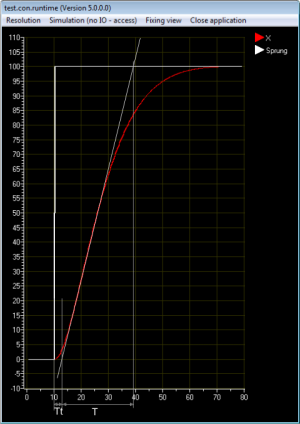
In Abb. 1 sehen Sie die ideale Sprungantwort eines PID-Reglers. Aus dem Bild wird die Bedeutung der einzelnen Parameter deutlich. Insbesondere die Bedeutung Tn als maßgeblicher Parameter für den I-Anteil ist gut zu erkennen. Hier wird auch deutlich, warum häufig Tn und nicht Ki als Parameter genutzt wird. Im realen Prozess kann man sich den Parameter Tn als Zeit allerdings besser vorstellen.
Beide Reglerstrukturen werden hier genutzt. Die Darstellung mit Tn und Tv wird häufig in Deutschland verwendet. Die Darstellung mit Ki und Kd ist im Angelsächsischen verbreitet. Es existieren drei unterschiedliche PID-Reglerimplementierungen. Im Abschnitt Sprungantwort der PID-Regler kann man das Verhalten der Regler gut vergleichen.
2.1 Was versteht man unter Nachstellzeit (Tn)?
Der I-Anteil eines Reglerausgangssignals sorgt für eine ständige Veränderung des Reglerstellgrades, bis der Istwert den Sollwert erreicht hat. Solange eine Regelabweichung besteht, wird der Stellgrad auf- bzw. abintegriert. Je länger eine Regelabweichung an einem Regler ansteht, desto größer wird der integrale Einfluss auf den Stellgrad. Je größer die Regelabweichung und je kleiner die Nachstellzeit ist, desto stärker (schneller) ist die Wirkung des I-Anteils. Der I-Anteil sorgt dafür, dass ohne bleibende Regelabweichung ausgeregelt werden kann. Die Nachstellzeit ist ein Maß dafür, wie stark die zeitliche Dauer der Regelabweichung in die Regelung eingeht. Eine große Nachstellzeit bedeutet einen geringen Einfluss des I-Anteils und umgekehrt. In der angegebenen Zeit Tn (in sec.) wird die Stellgrößenänderung, die der P-Anteil (xp oder pb) bewirkt, noch einmal aufaddiert. Somit besteht ein festes Verhältnis zwischen dem P- und I-Anteil. Wird der P-Anteil (xp) geändert, so bedeutet das auch ein geändertes Zeitverhalten bei einem gleichbleibenden Wert von Tn.
(Jumo.de: Was versteht man unter Nachstellzeit (Tn)?)
2.2 Was versteht man unter Vorhaltezeit (Tv)?
Über die Vorhaltezeit wird die Intensität des D-Anteils (Differentieller Anteil) eingestellt. Der D-Anteil eines Reglers mit PID oder PD-Struktur reagiert auf die Änderungsgeschwindigkeit des Istwertes. Beim Anfahren an den Sollwert „bremst“ der D-Anteil und kann damit ein Überschwingen der Regelgröße über den Sollwert vermeiden. Im Prinzip hat der D-Anteil folgende Auswirkungen: Sobald sich die Regelgröße verändert, wirkt der D-Anteil dieser Änderung entgegen. Für einen Regler mit einem inversen Wirksinn (also z. B. Heizen) würde dies beispielsweise bedeuten:
Verkleinert sich die Regelgröße aufgrund einer Störung in der Regelstrecke, bildet der D-Anteil einen positiven Stellgrad, welcher der Verkleinerung der Regelgröße entgegen wirkt. Vergrößert sich die Regelgröße aufgrund einer Störung in der Regelstrecke, bildet der D-Anteil einen negativen Stellgrad, welcher der Vergrößerung der Regelgröße entgegen wirkt. Je größer die Einstellung für die Vorhaltezeit (Wert in Sekunden) vorgenommen wird, umso größer ist das dämpfende Verhalten.
(Jumo.de: Was versteht man unter Vorhaltezeit (Tv)?)
3 PID-Regler: Kraftwerksregler (Implementierung 1)

Dieser Regler wurde maßgeblich durch das Zentrum für Forschung und Technologie (ZFT) im VEB EAW Berlin entwickelt und als Kraftwerksregler genutzt.
Im Wesentlichen zeichnet sich der Regler durch die spezielle Implementierung des D-Anteils aus.
Für die Aufschaltung des D-Anteils existiert ein extra Eingang (x). Im Normalfall wird der Eingang x auf das gleiche Signal wie der d-Eingang geschaltet. Experten können hier allerdings auch gezielt mit dem D-Anteil arbeiten.
Der D-Anteil ist als „realer“ D-Anteil mit einer Verzögerung implementiert (Siehe Idealer und realer PID-Regler).
Weitere Besonderheiten des Kraftwerksreglers
- stoßfreie Hand-/Automatikumschaltung
- stoßfreie Parameteränderung.
Dieser Regler arbeitet nach folgendem Algorithmus:
dYP=d-Wh
DYI=(d+Wh)*Ta/(2*Tn)
dYD=(X-Xh)*(10*exp(Ta/(Tv/10)))+YD*(exp(Ta/(Tv/10))-1)
YD=YD+dYD
Xh=X
Wh=ddY=(dYP+dYD+dYI)*Kr
Su=Su+dY;
Y=Su;
Hinweis: Der dargestellte Algorithmus entspricht nicht 1:1 dem C-Quellcode des Reglers, sondern ist eine vereinfachte Darstellung. Besonderheiten hinsichtlich Umschaltverhalten, wind-up usw. sind nicht enthalten.
Wichtiger Hinweis zum PID-Demo-Projekt in früheren Versionen
In den PID-Demo Applikationen wurde der Eingang x an die Regelgröße angeschlossen. Das ist 'falsch'. An den Eingang X muss in diesem Beispiel die Regeldifferenz (gleiches Signal wie an d) angeschlossen werden.
4 Universal- und Prozent-Regler (Implementierung 2 und 3)
Bibliothek PID-Controller (Float)(V3.0)
- PID-Controller (Percent)
- PID-Controller (Universal)
Die beiden Regler (Prozent und Universal) basieren auf dem gleichen mathematischen Basisalgorithmus:
esum = esum + e
y = Kp * e + Ki * Ta * esum + Kd * (e – ealt)/Ta
ealt = e
Hinweis: Der dargestellte Algorithmus entspricht nicht 1:1 dem C-Quellcode des Reglers, sondern ist eine vereinfachte Darstellung. Besonderheiten hinsichtlich Umschaltverhalten wind-up usw. sind nicht enthalten.
5 Sprungantwort der PID-Regler im Vergleich
Abb. 6 zeigt ein Anwenderprogramm, welches die Sprungantwort der unterschiedlichen Reglerimplementierungen im Vergleich darstellt. Für alle Regler werden identische Parameter genutzt. (Umrechnung der Parameter in die unterschiedlichen Darstellungsformen Tn→Ki; Tv-Kd)
Kr = 5
Tn = 10 (Sekunden)
Tv = 2
5.1 Testverlauf
Das Programm wird mit den konstanten Werten → Sollwert W=0 und Istwert X=0 in den Controller geladen.
Nach 10 Sekunden wird der Sollwert W auf 1 gesetzt (positives Sprungsignal).
5.2 Ergebnis
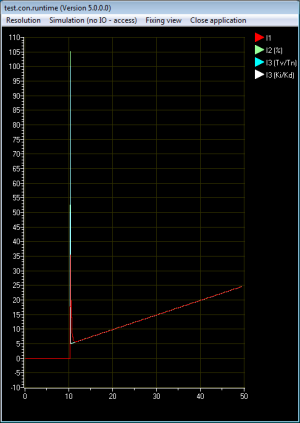
Wie zu erwarten war, zeigen die Diagramme (Abb. 6 und Abb. 7) ähnliche Kurven für alle Regler. Der Kraftwerksregler (I1 - rote Linie) verhält sich im D-Anteil etwas anders. Der Regler zeigt keinen idealen Sprung, sondern fällt in einer e-Funktion ab. Der Regler arbeitet also wie ein realer PID-Regler.
Vergleich mit Abb. 1 - ideale Antwort
Der Regler zeigt den erwarteten Signalverlauf.
- Nach dem Eingangssignalsprung reagiert der Regler mit einem sehr starken Impuls.
- Dann fällt der Impult bis auf den Kr-Wert
- Der Wert steigt dann alle 10 Sekunden (Tn) um den Kr-Wert
5.3 Parameteränderung während der Laufzeit
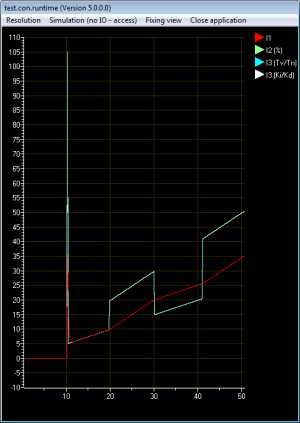
Während sich die 3 Implementierungen beim Sprung fast identisch verhalten, ist dies bei Parameteränderungen während der Laufzeit nicht mehr so. Sehr deutlich wird dies, wenn man die sich die Sprungantwort mit einer Parmeteränderung (Kr) ansieht.
- Kr wird nach 20 Sekunden von 5 auf 10 geändert
- Nach 30 Sekunden wird Kr wieder auf 5 gesetzt
- Nach ca 40 Sekunden wird Kr wieder auf 10 gesetzt
In einem zweiten Versuch wurde der Parameter Tn während der Laufzeit geändert. Das Bild ähnelt sehr stark dem Signalverlauf bei der Änderung von Kr.
- Tn wird nach 20 Sekunden von 10 auf 5 geändert
- Nach 30 Sekunden wird Tn wieder auf 10 gesetzt
- Nach 40 Sekunden wird Tn wieder auf 5 gesetzt
Ein Änderung von Tv hat keine Auswirkungen, da sich ja auch die Diffrenz zwischen W und X sich nicht ändert.
5.3.1 Ergebnis
Kraftwerksregler (Implementierung 1) mit stoßfreier Parameterumschaltung
In Abb. 8 sehen wir den Signalverlauf der Sprungantwort. Die rote Linie zeigt den Signalverlauf des Kraftwerkreglers (I1). Es ist zu erkennen, dass die Parameteränderung (Kr) am Ausgang zu keinem Signalstoß führt. Der Regler arbeitet im Geschwindigkeitsmodus, sodass sich der neue Parameter nur auf die Änderung der Differenz zwischen Soll- und Istwert auswirkt.
Regler (I2 und I3) mit stoßbehaftete Parameterumschaltung
Anders verhält es sich bei den Reglern (I2 und I3). Beide Regler verhalten sich identisch, daher gibt es auch nur eine Kurve für beide Regler. Die Parameteränderung hat eine unmittelbare Auswirkung auf das Ausgangssignal und führt zu einem Stoß im System. Dabei ist es egal, ob Kr oder Tn gändert wird. Entsprechend des Algorithmus haben beide Parameteränderungen änliche Auswirkungen. Y ist unmittelbar von Ki und dem Integral der Differenz abhängig. Anders als in der Implementierung des Kraftwerksreglers wirkt der Paramterer Ki auf das gesamte Integral des I-Gliedes. So ist auch die stärkere Wirkung der Parameteränderung nach längerer Zeit zu erklären. Da in Ki unmittelbar auch Kr steckt, wirkt sich die Änderung von Kr auch unmittelbar auf das I-Verhalten aus.
Ki = Kr/Tn
y = Kr * e + Ki * Ta * esum + Kd * (e – ealt)/Ta
Eine Änderung von Tv hat keine Auswirkungen, da sich Diffrenz bei einem Sprungsignal nicht ändert.
5.3.2 Warum diese unterschiedlichen Implementierungen?
Obwohl die stoßbehaftete Parameteränderung in realen Systemen zu Problemen führen kann, entspricht diese Implementierung der Erwartung des Anwenders. Wenn sich ein Parameter verdoppelt, erwartet der Anwender eine unmittelbare und heftige Reaktion des Reglers, da er die vereinfachte mathematische Formel im Kopf hat.
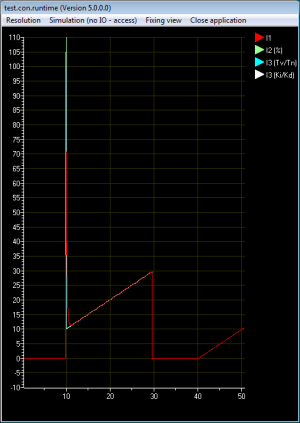
Testverlauf
- Nach 10 Sekunden wird ein Sprungsignal (1) auf den offenen PID-Regler gegeben.
- Nach 30 Sekunden werden die Regler auf Hand geschaltet (Yh = 0)
- Nach 40 Sekunden wird der Regler wieder auf Automatik geschaltet.
Ergebnis - Stoßfreie Hand/Automatikumschaltung
Alle drei Implementierungen verhalten sich bei der einfachen Hand/Automatikumschaltung identisch (siehe Abb. 9).
- Bei der Umschaltung auf Hand wird das Signal Yh = 0 auf den Ausgang Y gegeben.
- Zugleich wird die interne Summe der Regler auf den Yh-Wert abzüglich des Wertes aus dem P-Anteil gesetzt.
- Bei der Umschaltung auf den Automatikbetrieb startet der Regler auf dem voreingestellten Yh-Wert am Ausgang
- Im Automatikbetrieb wirkt zunächst nur der I-Anteil, da der P-Anteil aus der internen Summe herausgerechnet wurde.
6 Der geschlossene Regelkreis
Nun soll das Verhalten der einzelnen Reglerimplementierungen im geschlossenen Regelkreis betrachtet werden. Schauen Sie sich hierzu auch die deutsche Wikipediaseite „Faustformelverfahren (Automatisierungstechnik)“ mit den Faustregeln zum Einstellen an. Zur einfachen Parmeterbestimmung soll das Ziegler und Nichols-Verfahren genutzt werden.
Die Anwendung des Ziegler- und Nichols-Verfahren soll hier nicht als Empfehlung wahrgenommen werden. Es ist nicht unbedingt das optimale Verfahren. Das Verfahren dient nur zur Darstellung des Verhaltens der Regler.
(Wikipedia DE: Faustformelverfahren (Automatisierungstechnik)).
6.1 Sprungantwort der PT2-Strecke
In Abb. 10 sehen Sie die Sprungantwort der PT2-Strecke (PT2-Funktionsbaustein - TC=10; A=0.9). Der Kurvenverlauf wird entsprechend des gewählten Verfahrens ausgewertet.
Ergebnisse
Tt = 3 Sec.
T = 26 Sec.
6.2 Führungsverhalten als PI-Regler
Entsprechend der Faustformel wurden die Parameter für PI-Regler ermittelt und eingetragen.
Kr = 0.9/K * T/Tt = 7.8
Tn = 3.33 * Tt = 9.99
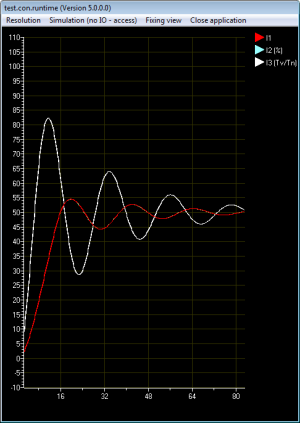
Abb. 11 zeigt das Verhalten der Regler
- Der Universalregler (I3) (Abb. 11 - weiße Linie) arbeiten ohne Begrenzung des Ausgangs - normalerweise wird der Ausgang entsprechend der realen Möglichkeiten des Stellgliedes begrenzt.
- Der Kraftwerkregler (I1) und der Prozentregler (Abb. 11 I1= rote Linie und I2 = grüne Linie) ist am Ausgang auf 0-100% begrenzt und kann daher nicht das volle Potenzial ausspielen.
Alle 3 Implementierungen (I1 bis I3) würden sich grundsätzlich identisch verhalten, wenn I3 ebenfalls auf 0-100 begrenzt werden würde. Die Regler schwingen weit über, da das Einstell-Verfahren nach ZN für ein Störverhalten und nicht für das Führungsverhalten genutzt wird. (Siehe Wikipedia DE: Regelkreis: Störverhalten eines Regelkreises)
6.3 Führungsverhalten als PID-Regler
Entsprechend der Faustformel nach ZN wurden die Parameter für die PID-Regler ermittelt und eingetragen.
Kr = 1.2/K * T/Tt = 10.3
Tn = 2 * Tt = 6
Tv = 0.5 * Tt = 1.5
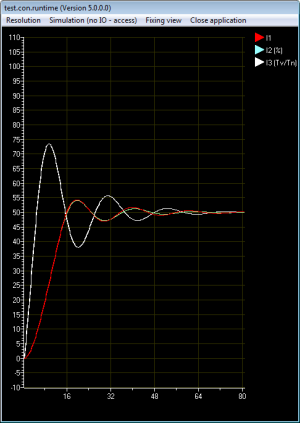
Abb. 12 zeigt das Verhalten der Regler
- Der Universalregler (I3) (Abb. 12 - weiße Linie) arbeiten ohne Begrenzung des Ausgangs
- normalerweise wird der Ausgang entsprechend der realen Möglichkeiten des Stellgliedes begrenzt.
- Der Kraftwerksregler (I1) und der Prozentregler (I2) (Abb.12 - I1 = rote Linie, I2 = grüne Line) ist am Ausgang auf 0-100% gegrenzt und kann daher nicht das volle Potenzial ausspielen.
Der PID-Regler schwingt schon nicht mehr so weit über wie der PI-Regler, da der D-Anteil dämpfend wirkt, obwohl Kr erhöht werden konnte und der Regler insgesamt schneller arbeitet.
6.4 Einstellregeln nach Chien, Hrones und Reswick
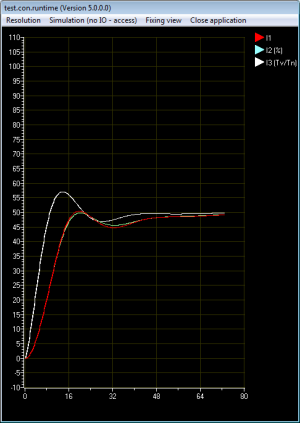
Ein besseres Führungsverhalten erreicht man, wenn man die Einstellregeln nach Chien, Hrones und Reswick nutzt.
Kr = 5.2
Tn = 26
Tv = 1.5
| Regler | Aperiodischer Regelverlauf | Aperiodischer Regelverlauf | Regelverlauf mit 20 % Überschwingen | Regelverlauf mit 20 % Überschwingen | |
|---|---|---|---|---|---|
| Störung | Führung | Störung | Führung | ||
| P | Kr | 0.3*(T/Tt*K)) | 0.3*(T/Tt*K)) | 0.7*(T/Tt*K)) | 0.7*(T/Tt*K)) |
| P | Kr | 0.6*(T/Tt*K)) | 0.35*(T/Tt*K)) | 0.7*(T/Tt*K)) | 0.6*(T/Tt*K)) |
| PI | Tn | 4*Tt | 1.2*T | 2.3*Tt | 1*T |
| PI | Kr | 0.95*(T/(Tt*K)) | 0.6*(T/(Tt*K)) | 1.2*(T/(Tt*K)) | 0.95*(T/(Tt*K)) |
| PID | Tn | 2.4Tt | 1*T | 2*Tt | 1.35*T |
| PID | Tv | 0.42*Tt | 0.5*Tt | 0.42*Tt | 0.47*Tt |
6.5 Störverhalten der Regler im Vergleich
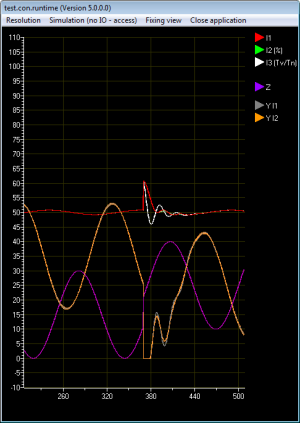
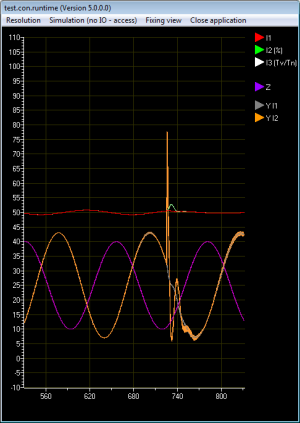
Abb. 14 zeigt das Störverhalten der Regler bei einer niederfrequenten sinusförmigen Störung. Die Lila-Linie zeigt das Störsignal, welches unmittelbar auf die Regelgröße aufgeprägt wird. Die überdeckende rote, weiße und grüne Linie zeigt die ausgeregelte Regelgröße. Die orange und überdeckte graue Linie zeigt das Stellsignal der Regler I2 und I1. Der heftige Ausschlag der Regelgröße rührt von Sprung des Störsignals um 25%. Alle drei Regler regeln den Störungssprung ähnlich gut aus.
Abb. 15 zeigt das Verhalten der Regler bei einer Parameteränderung. Während der Universalregler und der Prozentregler auf Parameteränderungen mit einem heftigen Ausschlag reagieren, macht sich eine Parameteränderung am Kraftwerksregler nicht bemerkbar.
7 Idealer und realer PID-Regler
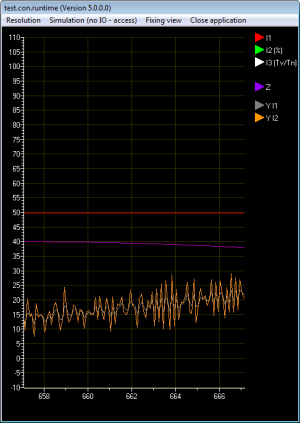
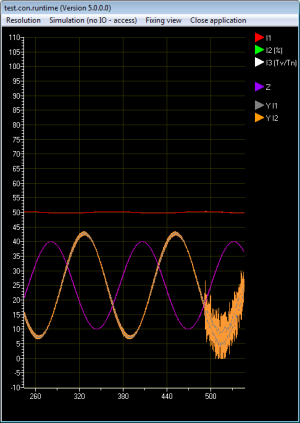
Bei einem idealen Regler hat der D-Anteil keine Verzögerung. Ein solches Verhalten ist in der Praxis aber nicht realisierbar und auch nicht erstrebenswert, da die Regeleinrichtung dann schon bei höherfrequenten Störungen kleiner Amplitude, die der Regelgröße überlagert sein können, zur Übersteuerung neigen würde. Die Implementierungen des Universalreglers (I3) und des Prozentreglers (I2) kommen dem Verhalten eines idealen Reglers allerdings weit näher als der Kraftwerksregler, da diese Implementierungen im Algorithmus selbst keine Verzögerung des D-Anteils besitzen. Selbstverständlich reagieren diese Regler in der Kombination mit dem Stellglied ebenfalls verzögert. Die Abbildungen 16 und 17 zeigen, dass der Universalregler (I3) und der Prozentregler (I2) auf höherfrequente Störungen relativ „nervös“ reagieren, während der Kraftwerksregler aufgrund seiner eigenen Verzögerung des D-Anteils wesentlich sanfter auf höherfrequente Störungen reagiert.