- General
- Introduction
- Controller structure
- Tn/Tv
PID Controllers
PID-Controller
PID-Controller (Percent)
PID-Controller (Universal)
What is a PID controller?
A proportional integral derivative controller (PID controller) is a control loop feedback mechanism (controller) commonly used in industrial control systems. A PID controller continuously calculates an error value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error over time by adjustment of a control variable, such as the position of a control valve, a damper, or the power supplied to a heating element.
(Wikipedia EN: PID controller)
You can find an example of a PID controller in the category Examples and Projects.
Controller Structure (Illustration Possibilities)
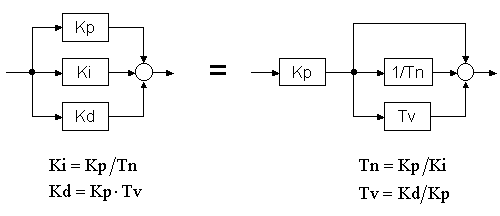
There are two possibilities to illustrate the controller structure, which are substantially identic. In analog measurement and control technology, the illustration with the reset time and derivative time is commonly used. The translation between both structures is possible with the given formula:
In image 1 you can see the ideal step response of a PID controller. From the image the meaning of each parameter becomes visible. Especially the meaning of the Tn as essential parameter for the I-term can be seen clearly. It also becomes obvious, why often Tn and not Ki is used as a parameter. However, in the real process it is easier to picture the parameter Tn as time.
Both controller structures are used here. The illustration with Tn and Tv is often used in Germany. The illustration with Ki and Kd is more common in English-speaking areas. There are three different PID controller implementations. In section Step response of PID controllers the behavior of the controllers can be compared very well.
What is a Reset time (Tn)?
The I-term of the controller output signal has the effect of continuously altering the manipulating variable, until the actual value has reached the setpoint.
As long as the control deviation is present, the manipulating variable is integrated upwards or downwards. The longer the control deviation continues to be present in a controller, the larger the integral effect on the manipulating variable. The larger the control deviation and the smaller the reset time, the more pronounced (faster) the effect of the I-term.
The I-term ensures the stabilization of the control loop without permanent control deviation. The reset time measures how much the duration of the control derivation effects the control action. A larger reset time means that the I-term is less effective and vice versa. Within the specified time Tn (in sec.), the change in the manipulating variable that is produced by the P-term (xp or pb), is added once more. Accordingly, there is a fixed relationship between the P- and the I-term. A change in the P-term (xp) also means a changed time response, at a constant value for Tn.
(Jumo.de: What is meant by reset time (Tn)?)
What is derivative time (Tv)?
The intensity of the D-term (differential term) can be set via the derivative time. The D-term of a controller with PID or PD action reacts to the rate of change of the actual value.
When the setpoint is approached, the D-term acts as a brake, thereby preventing the control variable from overshooting the setpoint.
Basically, the D-term has the following effects:
As soon as the control variable changes, the D-term reacts against this change.
For a controller with an inverse operating sense (i.e. for heating) this would mean, for example:
- If the control variable decreases as a result of a disturbance in the process, the D-term forms a positive manipulating variable, which counteracts the reduction in a control variable.
- If the control variable increases as a result of a disturbance in the process, the D-term forms a negative manipulating variable, which counteracts the increase in a control variable.
- The damping action increases with the size of the setting for the derivative time (value in seconds).
(Jumo.de: What is meant by derivative time?)